|
Umfassende Bereiche: |
|
Modebegriffe wie Selbstorganisation, Fraktale, Attraktoren beginnen philosophische und soziologische Literatur sowie populärwissenschaftliche Darstellungen von Natur- und Geisteswissenschaften zu überschwemmen. Bei aller - auch bei mir vorhandenen - Begeisterung für diese neuen Konzepte sollten wir uns bewußt bleiben, welche Substanz und welche Voraussetzungen in den Grundmodellen stecken, um nicht zu fehlerhaften "Kurzschlüssen" verleitet zu werden. Im Folgenden untermauere ich einige typische"Illustrationen" zur Darstellung komplexer, sich selbst organisierender Erscheinungen. |
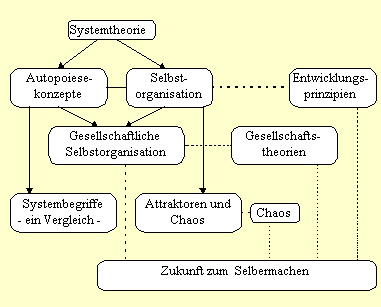
2. Strukturentstehung 3. Sprünge und Gebrochenes 4. Reale Bedeutung der Fraktale 5. Selbstorganisation 5.1. Konservative Selbstorganisation 5.2. Dispersive Selbstorganisation 5.3. Dissipative Selbstorganisation 6. SELBST-ORGANISATION im weiteren Sinne
Alle Bereiche der Welt sind relativ stabil. Stabil in Bezug auf die eigene Realisierung von inneren Wechselwirkungen, die für sie typisch sind und eine Zeitlang zyklisch und relativ unverändert ablaufen. Diese Stabilität ist aber nur relativ, weil die Wechselwirkungen auf Bedingungen treffen bzw. selbst die Bedingungen erzeugen, die Veränderungen hervorrufen.
"Organisation" hat die Doppelbedeutung: 1. Stabile Strukturen in ihrer Existenz und 2. Entstehen von Strukturen. Komplexe Strukturen erhalten sich selbst stabil, indem sie als Ganze ihre innere Struktur so organisieren, daß innere Teile untereinander und mit äußeren Strukturen wechsel-wirken. Die Prozesse der Wechselwirkung durch Teile im Innern erhalten das Ganze stabil. Die Teile müssen deshalb unterschiedlich sein, damit sie untereinander etwas auszutauschen haben (Spezialisierung, Differenzierung), aber sie müssen gleichartig genug sein, um miteinander Wechselwirkungen einzugehen.
Teile in Bezug zu einem Ganzen sind selbst Ganze in Bezug auf ihre innere Struktur und die Ganzen sind auch nur wieder Teile übergreifender Ganzer (Hierarchie). Das hat nur in menschlicher Interpretation etwas mit verdammenswerter Machtausübung zu tun, kennzeichnet lediglich die sog. "Selbstähnlichkeit" oder "Holografieartigkeit" der Welt. Eine Theorie, welche die Selbsterhaltung von komplexen Strukturen auf der Grundlage der Selbsterzeugung der eigenen Teile und des eigenen Randes betont, ist das Autopoiese-Konzept (für die Biologie) nach Maturana und Varela.
Im physikalischen Bereich wurde die "zyklische Kausalität" (Ganzes erzeugt Teile, die wiederum das Ganze erzeugen) durch die Synergetik von Hermann Haken gefunden.
Chemische dissipative Prozesse waren Ausgangspunkt für das Selbstorganisationskonzept nach Ilya Prigogine.
Alle Konzepte erlauben eine Übertragung typischer Strukturmodelle auf andere Gegenstandsbereiche und wurden deshalb als allgemeine Konzepte berühmt. Gewisse Streitigkeiten der Autoren um eine Vormachtstellung sind nicht sehr sinnvoll, es bietet sich immer wieder an, aus allen Konzepten Wesentliches herauszukristallisieren. Jedes Konzept kann seine besonderen Fähigkeiten an bestimmten typischen Aspekten demonstrieren.
Die Aufrechterhaltung realer Strukturen geschieht über Wechselwirkungsprozesse im Innern und im Austausch mit äußeren Strukturen. Diese Prozesse verändern die Bedingungen für ihre Wirkungsweise ständig selbst. Dadurch kommt es zu Veränderungen in der Prozeßrealisierung. Die Übergänge während der Veränderung von Strukturen in verschiedenen Bereichen sind nicht immer stetig. Stabile Strukturen unterliegen den für sie typischen (durch sie selbst realisierten) wesentlichen Zusammenhängen (Gesetzen). Sind diese Zusammenhänge durch die Bedingungsänderung nicht mehr realisierbar, müssen die beteiligten Strukturen sich neu ordnen, neu strukturieren. Das beinhaltet auch ihre innere Umgestaltung, Neugestaltung! Ganze und Teile müssen andere stabile Strukturen bilden oder (stofflich-energetisch) in andere Ganze aufgehen. Andere stabile Strukturen können (wenn die Bedingungen es zulassen) früheren Strukturzuständen entsprechen. Weil sich die Bedingungen aber irreversibel geändert haben, ist diese Regression oft nicht möglich. Dem Aufgehen in andere Strukturen entspricht die Beendigung ihrer Existenz ohne das "Mitnehmen" von Eigenem (der Tod).
Im günstigsten Fall gelingt der Aufbau stabiler neuer Strukturen auf Grundlage der neuen Bedingungen (unter "Aufhebung" früherer Eigenschaften). Diese neuen Strukturen unterscheiden sich aber deutlich von den früheren, es kam zu einem qualitativen "Sprung" an einem bestimmten Punkt der zeitlichen Entwicklung.
Die Situation, von der Entwicklung abhängt, ist die Wechselwirkung und das Zurückwirken von selbst-veränderten Bedingungen. Beides läßt sich mathematisch nur mit nichtlinearen Gleichungen darstellen, bei denen noch dazu in der zeitlichen Folge ein Prozeß die Ergebnisse des anderen wieder verwendet und so weiter...
Fraktale sind pure Mathematik
Fraktale (lat. Fractus - gebrochen) sind mathematische Gebilde mit gebrochen-zahligen Dimensionen. Bekannte Fraktaldarstellungen, wie das "Apfelmännchen" sind die grafische Darstellung der Lösungen eines iterativen Gleichungssystems. Sie hängen von zwei Koordinaten und zwei Variablensowie von den Startbedingungen für die Variablen und den Abbruchbedingungen für die Iteration. |
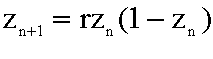
|
d.h.: das Ergebnis zn wird wieder in die nächste Rechnung eingesetzt... Das Bild spannt sich über die x-y-Ebene. |
|
Grafisch wird das zeitliche Verhalten der Lösung dargestellt: Je nachdem, nach wievielen Iterationsschritten die Gleichung konvergiert, oder ob sie divergiert oder oszilliert, erhalten die Funktionswerte eine definierte Farbe.
|
| Für die logistische Gleichung (s.o.) wird i.a. auch das Bifurkationsbild (in Abhängigkeit vom Parameter r) abgebildet. | 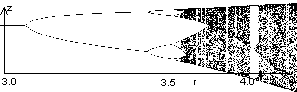
|
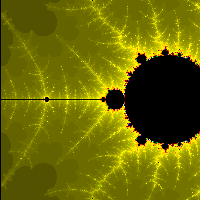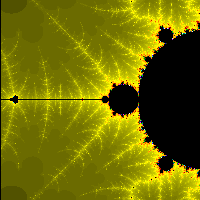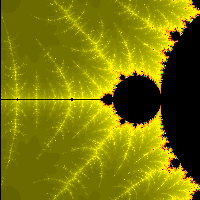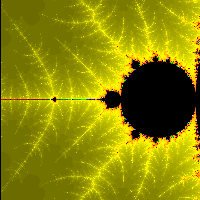
| Für eine bestimmte (etwas veränderte) Gleichung heißt die Lösungsmenge Mandelbrotmenge und wird auch "Apfelmännchen" genannt. Sein Rand ist ein Fraktal.

| 
|
| Die Fraktalentwicklung zum "Zuschauen" von Hanswerner Spring (http://www.fractalus.ch/animations/animations/anima_00.html) |
|
| Julia-Mengen entstehen ähnlich für jeden festen Punkt auf dem Fraktal selbst.
Den Farben entspricht die Anzahl der durchlaufenen Iterationszyklen.
Typische Eigenschaften sind: Im exakten mathematischen Sinne sind Attraktoren periodische oder geschlossene Trajektorien im zweidimensionalen Phasenraum. Bestimmte unregelmäßige Bewegungen in der dritten Dimension sind nicht mehr durch geschlossene oder periodische Attraktoren (im zweidimensionalen Phasenraum), sondern nur noch durch sog. "seltsame" Attraktoren abzubilden.
- Im chaotischen Bereich springen die Zustände (unvorhersagbar, weil extrem fein abhängig von den Anfangszuständen) zwischen den Attraktorbereichen umher, die Julia-Menge ist dann keine geschlossene Linie, sondern selbst wie Blätterteig (unstetig/ gebrochen) in sich geschichtet (Cantor-Menge).
4. Reale Bedeutung der Fraktale: Bedingungen wie:
- positive Rückkopplungen (Iteration) innerhalb eines zyklichen Prozesses oder durch die Wechselwirkung verschiedener Prozesse;
Deshalb gibt es in der Natur zwar keine "Fraktale" oder "Attraktoren" (wie es da auch keine "Dreiecke" gibt), aber durchaus vergleichbare Eigenschaften natürlicher Objekte:
- Sensibilität gegenüber bestimmten Bedingungsänderungen, vor allem in besonderen "sensiblen Phasen" (z.B. in der menschlichen Individualentwicklung),
Ab einem bestimmten Nahrungsangebot verhält sich die Population periodisch, bei weiterer Erhöhung des Nahrungsangebots verdoppelt sich die Periode in immer kleineren Abständen, ab einem bestimmten Wert tritt Chaos auf (R.May) (Hier ist der Parameter r die Menge des Nahrungsangebots).
Alle Erscheinungen, die dem mathematischen Bild der Fraktale in ihren Strukturen entsprechen, haben etwas mit Selbstorganisation zu tun.
Das Bild der Fraktale vereint stabile Bereiche ("Attraktoren") und sensible und chaotische Bereiche (seltsame Attraktoren, Julia-Mengen), Ordnung und Chaos - Chaos in der Ordnung sowie Ordnung im Chaos.
Im Bifurkationsbild werden mögliche Veränderungen in Strukturen sichtbar, wenn der Parameter mit der Zeit wächst (dann kann an Stelle des Parameters die Zeit eingetragen werden). Die Veränderungen führen in den "Bifurkationspunkten" zur Neuentstehung von neuen Strukturen.
Wenn die Parameteränderung durch den (existenztragenden) Prozeß selbst hervorgerufen wurde, ist die Entstehung des Neuen SELBST-organisiert.
"Chaos" gibt's an mindestens 4 Stellen:
Es darf auch nie vergessen werden, daß diese Bilder idealtypische Situationen zeichnen und überhaupt nichts über qualitative Inhalte von Strukturen und Prozessen aussagen.
5. Selbstorganisation
5.1. Konservative Selbstorganisation: - im thermodynamischen Gleichgewicht
- bei starken Wechselwirkungen (abgeschlossene Systeme: Vereisung des Wassers, Magnetisierung für abgekühltes Eisen) a) Nichtintegrabilität (d.h. mit Wechselwirkung, z.B. Planetensystem) mgl. chaot. Verhalten
b) Phasenübergänge : intermolekulare Wechselwirkungen
Das Maß im Phasenraum bleibt erhalten,
5.2. Dispersive Selbstorganisation
- Solitonen: impulsförmige Lösungen nichtlinearer partieller Differentialgleichungen, die lokalisierte, sich bewegende Strukturen eines Wellenfeldes mit hoher Stabilität beschreiben (Ebeling, Feistel 1986 S. 52).
5.3. Dissipative Selbstorganisation:
"Es tritt eine neue molekulare Ordnung auf, die im Grunde einer gewaltigen Schwankung entspricht, welche durch den Energieaustausch mit der Außenwelt stabilisiert wird."(Prigogine, Vom Sein zum Werden) - fern vom thermodynamischen Gleichgewicht
- Maß im Phasenraum bleibt nicht erhalten (Zeitinvarianz)
6. SELBST-ORGANISATION im weiteren Sinne: Sich selbst organisiertende Bereiche der Welt haben zwei typische Stadien: a) das autopoietische Sich-Selber-Reproduzieren in inneren zyklischen Prozessen auf Grundlage von Stoff-,Energie- und Informationsaustausch mit der Umwelt, (die dadurch automatisch zur "Mitwelt" wird). Dieser Zustand der Zyklizität ist aber nie ewig (wegen der Selbst-Veränderung der Bedingungen für die Prozesse, die an qualitative Begrenzungen stoßen... um diesen Satz zu begründen habe ich eigentlich das ganze erste Buch geschrieben). Es kommen (bzw. das System erzeugt selbst!) kritische Phasen, in denen es aufhört in der alten Form zu existieren. Es stirbt ab - oder organisiert sich neu.
Das ist b) die originäre "Selbstorganisation". Hier passiert (im angenommenen günstigen Fall) eine Innovation, der "Sprung" in einen neuen Zustand. Die Zyklizität bricht auf zur Spirale ins Offene, Neue. Eine Rückkehr in total frühere Zustände ist schon deshalb sowieso nicht möglich, weil die Bedingungen (durch den Lebensprozeß selbst!) verändert wurden.
Selbstorganisation als "irreversibler Prozeß, der durch das kooperative Wirken von Teilsystemen zu komplexen Strukturen des Gesamtsystems führt." (Ebeling, Feistel,1986)
Im engeren Sinne entstehen komplexe globale Muster durch einfache lokale Interaktionsregeln (Rojas, 1992). Bifurkationen (qualitative Veränderung der Struktur der zugrundeliegenden Wahrscheinlichkeitsverteilung) mit verschiedenen Formen:
- statisch oder dynamisch (dann Hopf-Bifurkation: strukturell stabil, nur Attraktor ändert sich) |
Bifurkation |
Bifurkation |
Singularität (mit äuß. Feldern) |
Komplexe Systeme brechen Zeitsymmetrie (Prigogine) Voraussetzung (nicht identisch mit!) für Evolution (Zeitdefinition aus Symmetriebrechung: mikrosopische Zufälligkeit makroskopische Irreversibilität) Zeit als innere Variable (nicht äußere Parameter) - neu gg. Relativitätstheorie: Zeit und Raum sind abhängig von Materiebewegung und zusätzlich noch miteinander verschränkt ("Verzeitlichung des Raumes")
- Zeit steckt in den Wechselwirkungs-"Erinnerungen" (Prigogine 1991)
Noch eine Erkenntnis, die dialektische (evolutive) Prozesse kennzeichnet und von den Selbstorganisationskonzepten unterschiedlich widergespiegelt wird:
Beim "Sprung" in neue Zustände gibt es zwei zu unterscheidende Hauptformen:
a) die mir eher unsympatische Koordinierung der Teile des Ganzen über die sog. "Versklavung" entsprechend des Synergiekonzeptes von H.Haken, wenn mans genau von seinen Quellen und Voraussetzungen her betrachtet (als Physikerin weiß ich ja, wie der Haken seine Formeln ausgehend vom Laser berechnet hat und was dann als nicht-mehr-genannte Voraussetzungen drinsteckt!) und bei der physikalischen Selbstorganisation (Benard-Zellen...). In diesem Fall sind die Teile typischerweise einheitlich, vom Wesen her untereinander nicht unterschieden.
"Langlebige (=instabile. d.i.: Zeitkonstante ist sehr groß, d.h. Dämpfung klein) Systeme versklaven kurzlebige (instabile) Systeme" (Haken)
b) die Integration unterschiedlicher Teile in einem neuen Ganzen (Hegel :"Identität der Identität und des Unterschieds") - hier entstehen die Teile in ihrer Spezifik in dem Ganzen sogar erst, enthalten gegeneinander genügend Unterschiede, um den das Ganze aufbauenden Austausch zu ermöglichen. Selbstorganisierende Systeme sind
-komplex, Dabei ist "die Interaktion von Selbstreferenz und Redundanz... die Quelle von innovativem Verhalten" (Erpenbeck 1989).
Reale sich selbstorganisierende Systeme beeinflussen ihre Umwelt auch selbst, so daß sie die auf sie einwirkenden Bedingungen selbst mit herstellen (Ko-Evolution der Systeme).
c) für noch höhere Werte des Nicht-Gleichgewichts-Parameters entstehen neue Instabilitäten, die irreguläre Bewegungen bedeuten Turbulentes Chaos. Literatur:
Briggs, J., Peat, F.D.: Die Entdeckung des Chaos. Eine Reise durch die Chaos-Theorie, Wien 1990
Ebeling, W., Feistel, R.: Physik der Selbstorganisation und Evolution, Berlin 1986
Annette Schlemm, 8.1.1997 für Gesprächsrunde am 10.1. und Buch Teil 2 sowie Internet
siehe auch:
Weiterhin lesenswert:
|