Die Frage der Dimensionen der Raumzeit wurde seit der Entdeckung des Minkowskiraums akut. Man kann die Gleichung für den Kegelschnitt (siehe Abbildung 6) auf folgende Weise herleiten:
Zuerst nennen wir die allgemeine Formel für die Metrik, die sich aus der Anwendung des Satz des Pythagoras (1) für drei Dimensionen ergibt:

dx12 + dx22 + dx32 - (cdt)2 = 0 Hier werden dreidimensionale Objekte so dargestellt, dass sie den Eindruck erwecken, sie würden sich bewegen; die Bewegungskomponente ist qualitativ von der Raumdimensionalität unterschieden: Abbildung 7: Paul Klee: "Nichtcomponiertes im Raum" 1929 (aus Müller (o.J.), S. 65)

dx12 + dx22 + dx32 + (icdt)2 = 0 Die Raumzeit wird als vierdimensionaler Raum dargestellt, in dem auf den Trick zurück gegriffen wird, dass z.B. dreidimensionale Objekte in den zweidimensionalen Raum hinein gefaltet werden können. Die 4. Dimension kann man derart in aufgefalteter Form im dreidimensionalen Raum andeuten - es entsteht ein sog. Hyperkubus (vgl. Banchoff 1991: 105ff.).   Abbildung 8: Theo van Doesburg 1925 (aus Müller (o.J.), S. 60)

Gegen die Gleichstellung der 4 Dimensionen wie in (10) sprechen allerdings einige physikalische Argumente[1] , wie die Inkongruenz der linken und der rechten Hand sowie das Auftreten von Dunkelheit nach dem Löschen eines Lichts (vgl. Kanitscheider 1991: 426).

Die Einsteinsche Feldgleichung der allgemeinen Relativitätstheorie ((5), mit k: Konstante) erfasst komplexe Zusammenhänge:
I. Das Gravitationsfeld und die metrische Struktur des Raumzeitkontinuums sind miteinander unauflösbar verbunden (linke Seite der Gleichung).
II. Die Krümmung/Gravitationswirkung (linke Seite) ist der Wirkung der nichtgeometrischen Materiefaktoren (rechte Seite) äquivalent.

Die mathematische Äquivalenz in II. sagt erst einmal nichts über eine kausale Verursachung. Die Form der Gleichung wurde aber bewusst in Anlehnung an die Poissonsche Feldgleichung der klassischen Physik[2] gewählt. Die Energie-Impulsdichte gilt dabei als Quelle der Erregung eines Gravitationsfeldes (Gleichheitszeichen), das in unserem Fall eng mit der metrischen Struktur der Raumzeit verbunden ist (linke Seite). Das Feld bestimmt dann wiederum die Bewegungsmöglichkeiten von Objekten.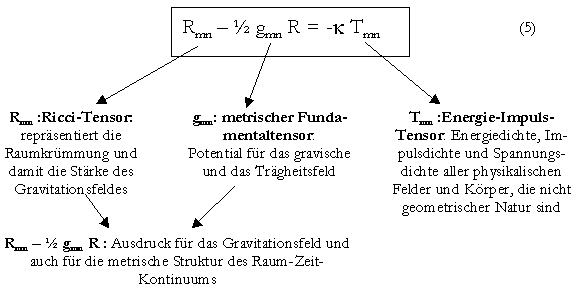

Der Zusammenhang von nichtgeometrisierter Materie (rechte Seite) und Gravitation und Metrik (linke Seite) ist nichtlinear: Raum und Zeit werden "durch das Schwerefeld bestimmt, während das Schwerefeld seinerseits von der Verteilung der Massen im Universum abhängt." (Renn 2006: 200) Abbildung 9: Abhängigkeit des Schwerefelds und der Raumzeitmetrik von der Masseverteilung(Quelle: Bublath 1999: 39)

Das Raumzeitkontinuum ist eng verknüpft mit den Eigenschaften der Materie - einerseits (auf der linken Seite der Gleichung) mit der gravitativen Wirkung, andererseits auch mit den anderen Materieformen (den nicht gravitativen, nicht geometrisierten auf der rechten Seite der Gleichung). Einstein fasste zusammen:

In der allgemeinen Relativitätstheorie gilt, dass der Raum[3] nicht mehr ein "starrer Bezugskörper" ist, sondern seine Metrik vom lokalen Gravitationsfeld abhängt. Diese Folge des allgemeinen Relativitätsprinzips beschreibt Einstein auch mit dem Wort "Bezugsmolluske" (Einstein 1920a: 67). Bloch paraphrasiert dies später:

Es stellt sich heraus, dass auch in der allgemeinen Relativitätstheorie die Raumzeit nicht vollständig in der materiellen Dynamik aufgehoben ist, sondern es eine Dualität von raumzeitlicher Metrik, die auch als Gravitationsfeld darstellbar ist (dem "Gravitationsäther"[4]) und nicht geometrisierbarer Materie gibt.
Eine weitere Fragestellung ergibt sich, wenn wir bedenken, dass wir nicht über irgend welche abstrakten Materieformen bzw. Raumzeiten sprechen, sondern dass wir Physik betreiben, also "eine Theorie, die auch zutreffen muß." (Treder 1999: 49) Es geht also darum, die physikalischen Bewegungsformen, die wir untersuchen, nicht nur spekulativ in einer mathematischen Form darzustellen - sondern diese Darstellung muss auf ihren Wahrheitsgehalt hin überprüfbar sein. Soweit es um raumzeitliche Bewegung geht, muss in Raum und Zeit gemessen werden können.
In der speziellen Relativitätstheorie ist die Definition der Gleichzeitigkeit immer nur für ein Inertialsystem möglich. Trotzdem, so hatten wir bereits gesehen, lassen sich Raum- und Zeitkoordinaten noch unmittelbar messen.
Diese unmittelbare Interpretation der Raum- und Zeitkoordinaten durch Maßstäbe und Uhren geht in der allgemeinen Relativitätstheorie verloren. Aber die Messbarkeit war für Einstein so wichtig, dass er den korrespondenzmäßigen Anschluss an die Messbarkeit im euklidischen Raum zur Richtschnur bei der Entwicklung der allgemeinen Relativitätstheorie verwendet hatte (vgl. Renn 2006: 271).

Hermann Weyl hatte versucht, diesem Dualismus zu entkommen, indem er auch den Längenmaßstab selbst mit veränderte (vgl. Weyl 1921: 224). Dem wiedersprach jedoch Einstein. In der Rezension eines Buches von Weyl schrieb er:

Mit diesem Zustand des Dualismus von Raumzeit und Materiedynamik war Einstein letztlich nicht zufrieden:

Bisher wurde meist angenommen, so etwas wie physikalische Teilchen, Kräfte oder Felder könne man als real existierend annehmen, beim Raum gab es Streitigkeiten, ob es ihn real gibt oder ob er lediglich eine ideelle Denkvoraussetzung sei. Jetzt erweist sich ein Teil der Wirklichkeit, das Gravitationsfeld und die Metrik als ineinander umwandelbar, als wesensgleich.
Wenn wir als "real" das definieren, was invariant ist, so würde das Gravitationsfeld bzw. die Metrik diese Zuschreibung durch die Allgemeine Relativitätstheorie verlieren. Wir erwähnten bereits das mentale Modell des Menschen in einem frei fallenden Kasten ("Aufzug"), bei dem durch die Fallbewegung die Wirkung des Gravitationsfeldes gerade aufgehoben wird. Wenn wir also ein mitbewegtes Bezugssystem wählen, haben wir das Gravitationsfeld "wegtransformiert", es ist nicht invariant, also nicht "real" (vgl. Kanitscheider 1991: 175). Bei dieser Sichtweise bleibt ein anderes Moment der Gravitation real: die Gravitationsgezeitenkraft.

In einem homogenen Gravitationsfeld besagt das Äquivalenzprinzip, dass es für einen Menschen in einem geschlossenen Kasten ("Aufzug") nicht möglich ist zu unterscheiden, ob er Trägheitskräften oder der Gravitation unterliegt. Als mentales Modell hierfür dient auch die Vorstellung, dass in einem frei fallenden Aufzug die Gravitationskraft durch die Trägheitskraft aufgehoben wird. Insofern kann die Trägheitsbewegung in eine Gravitationsbewegung umtransformiert werden (bzw. umgekehrt). In einem nicht homogenen Gravitationsfeld (wie in Abbildung (10)) fallen die Massenpunkte nicht entlang paralleler Geodäten, sondern die Bahnen konvergieren. Diese Bewegung "aufeinander zu" kann in keinem Bezugssystem wegtransformiert werden. und ist Ausdruck der durch die Gravitation veränderten Geometrie der Raumzeit. Abbildung 10: Gravitations-Gezeitenkräfte(aus Bublath 1999: 91)

Legen wir jedoch eine andere Bestimmung von "Realität" zugrunde, nämlich diejenige, nach der real ist, was wirkt, so erhalten wir eine andere Sichtweise. Ian Hacking sagte über die Realität von Quarks: "If you can spray them, then they are real" (Hacking 1994: 22). In diesem Sinne wäre der sog. "Gravitationsäther", also die Einheit Gravitationsfeld/Metrik durchaus real, denn er bestimmt das physikalische Geschehen mit (vgl. Einstein 1920b: 317).

Die Feldgleichung der allgemeinen Relativitätstheorie macht lediglich lokale Aussagen. Sie hat auch nicht nur eine Lösung, sondern als System von zehn nichtlinearen Differentialgleichungen zweiter Ordnung für g_mn können sehr viele verschiedene Lösungen berechnet werden, von denen nicht alle physikalisch sinnvoll interpretierbar sind. Wie diese Grundgleichung sich im realen, globalen Weltraum auswirkt, ist eine zusätzliche Fragestellung (vgl. Einstein 1951/1979: 109). Weil die Feldgleichungen allein keine Aussagen über das großräumige Universum machen, lassen sich durch die Einbeziehung unterschiedlicher zusätzlicher Annahmen (z.B. über die Homogenität und Isotropie der Materieverteilung) verschiedene Lösungen errechnen, die dann mit der Wirklichkeit verglichen werden müssen. Einstein hatte zuerst eine Lösung gefunden, die für ein statisches Weltall sprach, wie er es auch erwartete. Jedoch fand der sowjetische Physiker Alexander Friedmann 1922 eine andere Lösung für einen nichtstationären Kosmos. Später wurde die Expansion des Weltalls auch experimentell bestätigt. Dabei gilt weiterhin, dass es 1. keine eineindeutige Beziehung zwischen dem Materie-Energie-Tensor und der Raummetrik gibt und 2. die globalen Eigenschaften sowie die Topologie des Raums sich daraus auch nicht ergeben. Durch die Einbeziehung von weiteren Zusatzannahmen ergeben sich vielfältige Lösungen der Einsteinschen Feldgleichungen.
Hans Jürgen Treder entwickelte in den 90er Jahren eine Kritik an diesem Vorgehen. Er folgte darin Ernst Mach, für den es keine Trennung zwischen Grundgleichungen und kontingenten Anfangs- und Randbedingungen geben darf.

In einer historischen Darstellung der Entwicklung der Relativitätstheorie ist dem sog. Machschen Prinzip eine große Bedeutung zuzuschreiben. Es war ein wichtiges heuristisches Prinzip für Einstein, obwohl es in seiner Theorie letztlich nicht gänzlich verwirklicht werden konnte. Die Debatte um das Machsche Prinzip beinhaltet gerade die Frage nach dem Verhältnis von physikalischer Materie und Raumzeit.
Ernst Mach hatte sich, wie viele andere, am absoluten Raum von Newton gestört. Er meinte: "Bleibt man auf dem Boden der Tatsachen, so weiß man bloß von relativen Räumen und Bewegungen." (Mach 1883/1921: 226). Er versuchte das Newtonsche Eimerexperiment (siehe Abbildung 3) auf eine alternative Weise zu erklären. Newton sah darin die Wirkung des absoluten Raumes realisiert. Mach wollte diese aus seiner Sicht abstrakte Konstruktion unnötig machen und verwies auf die Möglichkeit, die Trägheitsbewegung des Wassers im Eimer durch die Wirkung von Kräften aus dem gesamten Universum zu erklären. Die Trägheitskräfte sollen nicht durch Beschleunigung gegenüber dem absoluten Raum, sondern gegenüber den Hintergrundmassen im Universum zustande kommen. "Wenn wir daher sagen, daß ein Körper seine Richtung und Geschwindigkeit im Raum beibehält, so liegt darin nur eine kurze Anweisung auf die Beachtung der ganzen Welt." (ebd.: 227) Einstein reihte das "Machsche Prinzip" als dritten Hauptgesichtspunkt seiner Theorie neben dem Relativitäts- und dem Äquivalenzprinzip ein (Einstein 1918b: 241). Dieses Prinzip bedeutet, "daß das G-Feld[5] durch den Energietensor der Materie bedingt und bestimmt sei (ebd.: 242), d.h. auch: "Das wahre metrische Feld g_mn muß ganz durch die Materie der Welt bestimmt sein" (Einstein 1922/1979: 66), d.h. d.h. die Metrik muss in eindeutiger Weise aus Energie und Impuls der Materie im Universum hervorgehen. Der Dualismus von Raumzeit und Dynamik wäre dann aufgehoben. Nach Kanitscheider (1991: 170) kann das für die Feldgleichung Verschiedenes bedeuten:

• in Abwesenheit von Materie (T_mn -> 0) ist kein Gravitationsfeld möglich (d.h. die Metrik degeneriert g_mn -> 0)[6],
• in Abwesenheit von Materie wird die Metrik minkowskisch (g_mn -> h_mn)[7],
• in Abwesenheit der Materie verschwindet die Krümmung (R^a_bgd -> 0) oder
• es gibt keine Vakuumgleichungen.

Wie schon erwähnt, war Einstein unzufrieden mit der Dualität der linken und der rechten Seite seiner Feldgleichung (5). Der weitere Weg wurde von ihm und auch nach seinem Tod von anderen Wissenschaftlern in weiteren Vereinigungsversuchen gesehen. Eins dieser Programme war die Geometrodynamik nach Wheeler in den 60er Jahren (Wheeler 1962). Das Machsche Prinzip hatte die Vereinheitlichung von Raumzeit und dynamischer Materie durch die Abschaffung der Raumzeit versucht - in der Geometrodynamik sollte die Materie auf die Geometrie zurückgeführt werden. Es wurde vermutet, dass alle nichtgeometrischen Materieformen aus der Krümmung einer geeigneten Geometrie abgeleitet werden können. Dies war der Versuch, die "materielle Welt aus leerem gekrümmten Raum aufzubauen" (Kanitscheider 1991: 429). Da Vereinheitlichungen in der physikalischen Theorie bedeuten, in vorher getrennten Bereichen ein gemeinsames Wesen aufzufinden, wurde bereits spekuliert, dass "in den geometrischen Strukturen [...] das Wesen physikalischer Prozesse zutage [tritt]." (Griese 1966: 76) Innerhalb der Geometrie ergäbe sich jedoch auch hier eine Art Dualismus, und zwar jener zwischen Metrik und Topologie (Von Borzeszkowski, Wahsner 1979: 215).
In den 70er Jahren erwies sich dieses Projekt in dieser Weise als nicht realisierbar. Neue Theorien wie die String- und die Looptheorie entstanden, wobei sich neue Ideen und Begriffe entwickelten, die nicht mehr einfach in das alte Konzept einzuordnen waren. Die Loop-Theorie ist dabei eine Art "Erbe" der Geometrodynamik.

Stringtheorie

Die derzeit aktuellsten Kandidaten für eine neue Theorie, die alle bekannten physikalischen Wechselwirkungen vereinigt, sind die String- und die Looptheorie. In der Stringtheorie wird angenommen, dass die kleinsten Objekte, aus denen sich die Elementarteilchen aufbauen, nicht punktförmige Objekte, sondern Wellen auf linienförmigen Objekten, nämlich den "strings" (auf dt.: Schnur, Saite) sind. Diese Theorie erfordert nicht nur die bekannten 4 Dimensionen, sondern 10 und in ihrer weiter entwickelten Form als M-Theorie 11 Dimensionen. Genau so, wie die Anzahl der prognostizierten Elementarteilchen immer weiter zunahm, so entstehen auch in der Stringwelt immer neue Konzepte von Objekten, so z.B. auch zweidimensionale "Brane" (von "Membrane"). Obwohl wir selbst nur auf einer Membran leben und auch Licht und alle physikalischen Wechselwirkungen außer der Gravitation für uns auf diese eine Membran beschränkt sind, könnte die Gravitation zwischen den Branen wirken. Daraus lassen sich Experimente mit Messungen ableiten, die aber noch nicht genau genug durchgeführt werden können, um diesen eventuellen Einfluss zu messen. Um Effekte der zusätzlichen Dimensionen entdecken zu können, wird auf Teilchenbeschleunigerentdeckungen gesetzt.
Die Strings und Brane bewegen sich nach wie vor in einer voraus zu setzenden Raumzeit, auch wenn diese nun 11-dimensional ist. Lediglich eine von Hawking entwickelte Variante könnte auf einen "Außenraum" verzichten (Hawking 2003: 207).

Prägeometrische Looptheorie

Seit Ende der 80er Jahre wurden alte Gedanken von Wheeler und Penrose aufgegriffen und ein anderes Konzept einer erweiterten Theorie vorangetrieben. Es ist die Theorie der Quantengeometrie, auch Loop Quantum Gravity (Loop: Schleife) genannt. John Wheeler hatte in den 60er Jahren bereits vorgeschlagen, die Raumzeit in den kleinsten Bereichen als "schaumförmig" anzusehen, d.h. den Raum als ebenso gequantelt wie die Materie zu betrachten. Roger Penrose entwickelte in den 70ern sog. "Spin-Netze", die als Grundlage für eine Art "Raumzeit-Staub" zu verstehen waren. Raum und Zeit gelten dabei nicht mehr als vorauszusetzendes Medium, sondern sie werden als Folge des Aufeinanderwirkens der Elemente in "Spin-Netzwerken" erklärt (vgl. Zimmermann 1991: 46ff.). Raum und Zeit entstehen aus quantenphysikalischen Überlagerungen aller möglichen Zustände im Geflecht des Spin-Netzwerks. Solch ein Netzwerk kann es schon "vor" dem Urknall gegeben haben und aus ihm heraus entstand "beim" Urknall erst unser raumzeitliches Universum ("Initialemergenz"). Mittlerweile wurden bereits die mathematischen Voraussetzungen weit entwickelt, um Bewegungen und Kräfte zu beschreiben, ohne eine Hintergrundmetrik zu benötigen (basierend auf der mathematischen Knotentheorie).
Demnach besteht die tiefste Fundierung unserer Welt auf einem nicht raumzeitlichen Netzwerk von bestimmten Größen, die auch als "Twistoren"[9] bezeichnet werden; daraus entsteht eine raumzeitliche Geometrie. Als physikalische Materie bilden sich Anregungen in dieser Geometrie heraus (vgl. Geometrodynamik). Da Geometrie und auch Materie quantisiert sind, können sich Geometrie- und Materiequanten auch ineinander umwandeln, was für Schwarze Löcher angenommen wird. In diesen Konzepten werden ebenfalls Aussagen über beobachtbare Folgen der diskreten Raumzeit gemacht, vor allem bei der Beobachtung von Gammastrahlen-Ausbrüchen (Smolin 2004: 62).

Rainer E. Zimmermann geht - die philosophischen Konzepte von Spinoza und Schelling sowie die physikalischen Ideen von Wheeler und Penrose präzisierend - davon aus, dass nur die mit Massen, Längen und Zeiten bestimmbaren Objekte als "Welt" zu verstehen sind Das bedeutet, dass die Überlegungen zur Grundlegung von Raum und Zeit keine Themen innerhalb der Welt darstellen, sondern zu ihrem Grund, den er mit Spinoza und Schelling Substanz nennt. (Zimmermann 2004: 447, 476) Die Vereinigung von allgemeiner Relativitätstheorie und Quantentheorie erfolgt also nicht innerhalb der Welt, sondern außerhalb, wobei der Grund selbst raum- und zeitlos ist (ebd.: 266ff.). Es geht also hier um eine "Prä-Geometrie" (ebd.: 310), die diskontinuierlich und ohne Metrik ist. "Der Kosmos wird dabei beschreiben als eine bloße lokale Verwerfung des globalen Netzwerks, an der Initialsingularität auftauchend, in der Zeit seiend, und - möglicherweise - in einer Endsingularität wieder in die Raum-Zeitlosigkeit verschwindend." (Eisenhardt, Kurth 1993: 24) Aus den prägeometrischen Strukturen heraus entstand unsere Welt aus einer "Initialemergenz", die als "Brechung der Zusammenhangsstruktur eines Vorzustands" (Kurth 1997: 270) beim Übergang in die raumzeitliche Existenz unseres Universums zu verstehen ist. Dabei sind mathematische Strukturen und Operationen in der Diskussion, die diesen Prozess nachzeichnen sollen, und es wird durchaus nach der "ontischen Referenz" dieser mathematischen Größen gefragt (Eisenhardt, Kurth 1993: 38), aber in dem Sinne, dass uns bewusst ist dass wir sie nicht wahrnehmen oder messen können (Zimmermann 2004: 494, 497).

Wir Menschen sind in diesem Konzept Teil der Welt, aber nicht ihres Grundes, der Substanz. Wir erleben die Welt in Raum und Zeit, innerhalb dieser betreiben wir die empirische Physik, die unserer experimentellen Erfahrung zugänglich ist. Darüber hinaus erfordert jedoch die tiefere Begründung von weltlicher Materie, Raum und Zeit eine andere Art Physik, eine fundamentale Physik, die gleichzeitig als spekulative Philosophie (im Sinne Schellings) zu verstehen ist. (ebd.: 518). Trotzdem gibt es keine absolute Trennung zwischen Welt und Grund, empirischer Physik und fundamentaler Physik bzw. spekulativer Philosophie. Worin besteht der Zusammenhang? Spin-Netzwerke gehören noch zur welthaften Physik, sie sind quasi ihr "Rand". Der Zusammenhang zu ihrem nicht mehr welthaften, d.h. nicht mehr physikalisch erkennbaren substantiellen Grund ist eben in dieser Begründung zu sehen: Die den Grund erfassende spekulative Phantasie muss Bezug auf das nehmen, was über die Welt mindestens bereits gewusst wird (ebd.: 483).

Fußnoten:

[1] Einstein betont, dass die Gleichwertigkeit der Zeitkoordinate eine formale, aber keine physikalische ist (Einstein 1920d: 263f.)

[2] Die Poissonsche Gleichung besagt für die klassische Physik, "daß das Gravitationsfeld durch die Dichte r der ponderablen Materie erregt wird." (Einstein 1922/1979: 81)

[3]Der "Raum" meint auch im Weiteren immer die "Raumzeit".

[4] Zum Unterschied dieses Begriffes "Äther", das auch Einstein (1920b) verwendet, siehe Weyl (1922: 324).

[5]Als G-Feld bezeichnet Einstein den durch den Fundamentaltensor (der die metrischen Eigenschaften des Raumes sowie die Gravitationswirkungen bestimmt) Raumzustand (Einstein 1918b: 141).

[6] So formuliert es Einstein: Es darf "kein G-Feld möglich sein ohne Materie" (ebd.: 142).

[7] vgl. Schmutzer 1981: 106.

[8] Nur wenn das kosmologische Glied hinzugefügt wird, gilt die erste Variante (ebd.).

[9] Twistoren berücksichtigen im Unterschied zu Spinoren weitere "realistische" Parameter wie Bahndrehimpuls und Translation sowie die Relativistik der Bewegungen (vgl. Zimmermann 1991: 49).